第一册

集合

N = {0,1,2,3,……} (自然数集)

$Z = \{0,\pm1,\pm2,\pm3\}$ (整数集)

Q = {整数与分数} (有理数集)

R = {数轴上所有点对应的数} (实数集)

属于：$\in$
不属于：$\notin$

子集：$\subseteq$
真子集：$\subsetneqq$

指数函数与对数函数

根式：

$a^0=1(a\not=0)$
$a^{-n}=\frac{1}{a^n}$
$a^{m} \div a^{n}=a^{m} \cdot a^{-n}=a^{m-n}$
$(\frac{a}{b})^{n}=a^{n} \cdot b^{-n}=\frac{a^{n}}{b^{n}}$

分数指数幂：

分母上是几就是开几次方，分子则是乘几次方

$a^{\frac{m}{n}}=\sqrt[n]{a^m}$ $(a^{\frac{1}{n}}=\sqrt[n]a)$
$a^{-\frac{m}{n}}=\frac{1}{a^\frac{m}{n}}$

有理数指数幂运算法则：

$a^m\cdot a^n=a^{m+n}$
$(a^m)^n=a^{mn}$
$(ab)^n=a^n\cdot b^n$

对数：

$a^b=N\Leftrightarrow\log_aN=b$ （可以理解为b和N互换了位置，N把a踩扁了）
$\log_{10}N=\lg N$
$log_e N=ln N$ （e=2.71828……）

对数的运算法则：
$\log_aMN=\log_aM+log_aN$
$\log_a\frac{M}{N}=\log_aM-log_aN$
$\log_aM^n=n\log_aM$
对数的换底公式：
$\log_bN=\frac{\log_aN}{\log_ab}$
通常用常用对数进行换底，比如 $\log_{10}$
$\log_8 9\times\log_{27}32=\frac{\lg9}{\lg8}\times\frac{\lg32}{\lg27}=\frac{2\lg3}{3\lg2}\times\frac{5\lg2}{3\lg3}=\frac{2}{3}\times\frac{5}{3}=\frac{10}{9}$

第二册

第五章 数列

等差数列：

通项公式：
$a_n=a_1+(n-1)d$
等差中项：
$A=\frac{a+b}{2}$
前n项和公式：
$S_n=\frac{n(a_1+a_n)}{2}$ （就是小学背过的：首项加末项乘以项数除以二）

等比数列：

通项公式：
$a_n=a_1\cdot q^{n-1}$
$a_n=a_m\cdot q^{n-m}$ （两个公式本质上是一样的）
中项：
$G=\pm\sqrt{ab}$
前n项和公式：
$S_n=\frac{a_1(1-q^n)}{1-q}$
$S_n=\frac{a_1-a_nq}{1-q}$ (知道n时用这个公式)

第六章 三角函数

任意角的三角函数：

正弦：$\sin \theta=\frac{y}{r}$
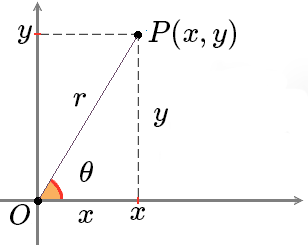
余弦：$\cos \theta=\frac{x}{r}$
正切：$\tan \theta=\frac{y}{x}$

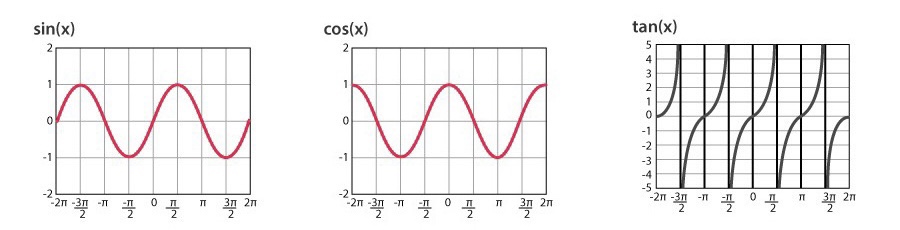
特殊角的三角函数值：

	$0^\circ$	$30^\circ$	$45^\circ$	$60^\circ$	$90^\circ$	$120^\circ$
$\sin\alpha$	0	$\frac{1}{2}$	$\frac{\sqrt2}{2}$	$\frac{\sqrt3}{2}$	1	$\frac{\sqrt3}{2}$
$\cos\alpha$	1	$\frac{\sqrt3}{2}$	$\frac{\sqrt2}{2}$	$\frac{1}{2}$	0	$-\frac{1}{2}$
$\tan\alpha$	0	$\frac{\sqrt3}{3}$	1	$\sqrt3$	不存在	$-\sqrt3$

第七章 平面向量

向量的加减：

加法：$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$
减法：$\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{BA}$
在坐标中：
$a+b=(x_1+x_2,y_1+y_2)$
$a-b=(x_1-x_2,y_1-y_2)$
$\overrightarrow{AB}=(x_2-x_1,y_2-y_1)$

平面向量位置关系：

平行（共线）：
$\overrightarrow{a}=\lambda\overrightarrow{b}\Leftrightarrow x_1y_2-x_2y_1=0$
垂直：
$\overrightarrow{a}\cdot\overrightarrow{b}=0\Leftrightarrow x_1x_2-y_1y_2=0$

向量的内积：

$\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}|\cdot|\overrightarrow{b}|\cdot\cos\theta$
内积坐标表示：
$\overrightarrow{a}\cdot\overrightarrow{b}=x_1x_2+y_1y_2$

向量的模长：

$|\overrightarrow{a}|=\sqrt{x^2+y^2}$

两向量夹角的余弦值：

$\cos\theta=\frac{\overrightarrow{a}\cdot\overrightarrow{b}}{|\overrightarrow{a}|\cdot|\overrightarrow{b}|}=\frac{x_1x_2+y_1y_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}$

AB两点之间的距离：

$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ （其实就是向量的模长)

AB中点坐标：

$(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$

第八章 直线与圆

直线的倾斜角：

一条与x轴相交的直线，逆时针方向与x轴形成的角，叫做直线的倾斜角

直线的斜率：

$k=\tan\alpha$
在坐标中：
$k=\frac{y_2-y_1}{x_2-x_1}$

直线方程：

点斜式方程：
$\frac{y-y_1}{x-x_1}=k\Rightarrow y-y_1=k(x-x_1)$ （已知斜率和点）
斜截式方程：
$y-b=k(x-0)\Rightarrow y=kx+b$ （k是斜率，b是直线在y轴上的截距）
一般式方程：
$Ax+By+C=0$

两直线位置关系：

两条直线有斜率且不重合，如果斜率相等，则两直线平行
$l_1\ /\mskip-4mu/\ l_2\Leftrightarrow k_1=k_2\ ,\ b_1\not=b_2$

解法一：$\frac{A_2}{A_1}=\frac{B_2}{B_1}\not=\frac{C_2}{C_1}$
解法二：将方程化成斜截式，比较$k_1=k_2\ ,\ b_1\not=b_2$

两条直线都有斜率，如果斜率互为负倒数，则两直线垂直
$l_1\perp l_2\Leftrightarrow k_1=-\frac{1}{k_2}\Leftrightarrow k_1k_2=-1$

$A_1A_2+B_1B_2=0$

两条直线相交条件：
$k_1\not=k_2\ ,\ \frac{A_2}{A_1}\not=\frac{B_2}{B_1}$

两直线交点坐标：
解：

$\left\{ \begin{aligned} A_1x+B_1y+C_1=0 \\ A_2x+B_2y+C_2=0 \end{aligned} \right.$

点到直线的距离：

$d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$

两平行线的距离：

$d=\frac{|C_2-C_1|}{\sqrt{A^2+B^2}}$

圆：

圆的标准方程：
圆心为$A(a,b)\ ,\ P(x,y)$是圆上任意一点
$(x-a)^2+(y-b)^2=r^2$

圆的一般方程化为标准方程（配方法）：
$x^2+y^2-2x+4y-11=0$
$(x-1)^2+(y+2)^2-1-4-11=0$
$(x-1)^2+(x+2)^2=16$

直线与圆位置关系：
用点到直线方程求直线到圆心的距离

第三册

第十三章 立体几何

球：

球的体积：
$V=\frac{4}{3}\pi R^3$
球的表面积：
$S=4\pi R^2$

See More

一开始我只是想把数学笔记写到个人博客上
但是使用 Markdown 拓展语法把数学公式公式写出来后，却发现并不能在网页上正常渲染
试过很多办法，最后是找到了一个叫vuepress-plugin-katex (opens new window)的插件，然后又想办法给他配置上
总共花了我一个下午的时间
……
怎么感觉像是为了一碟醋包了盘饺子